 พีทาโกรัส (582 — 496 ปีก่อนค.ศ.; กรีก: Πυθαγόρας) เป็นนักคณิตศาสตร์และนักปราชญ์ชาวกรีกโบราณ, เป็นที่รู้จักในนามเจ้าของทฤษฎีบทพีทาโกรัส
พีทาโกรัส (582 — 496 ปีก่อนค.ศ.; กรีก: Πυθαγόρας) เป็นนักคณิตศาสตร์และนักปราชญ์ชาวกรีกโบราณ, เป็นที่รู้จักในนามเจ้าของทฤษฎีบทพีทาโกรัสประวัติ
พีทาโกรัสเกิดเมื่อ 559 ก่อนคริสต์ศักราช ที่เมืองซามอส (Samos) ประเทศกรีซ (Greece)[1] และเป็นบุตรชายของพีทาอิส และ เนซาร์คัส พีทาโกรัสได้ออกจากบ้านเกิดเมืองนอนของเขาไปที่โครโทน (Croton) ในทางใต้ของอิตาลีเมื่อเขาเป็นชายหนุ่ม เพื่อที่จะหลีกหนีจากรัฐบาลทรราชของโพลีเครติส และผู้เชี่ยวชาญหลายคนคาดคเนว่าก่อนที่พีทาโกรัสถึงเมืองโครโทนนั้น เขาได้เยี่ยมเยียนนักปราชญ์ของอียิปต์และบาบีโลนก่อน เมื่อเขาได้ย้ายถิ่นฐานจากซาโมสมายังโครโทน พีทาโกรัสก็ได้ก่อตั้งสมาคมศาสนาลับ ที่คล้ายคลึงกับลักธิออร์เฟอัสที่มีอยู่ก่อนหน้านั้น
ณ เมืองโครโทนพีทาโกรัสได้จัดปฏิรูปวัตนธรรมของชาวโครโทน โดยแนะให้ชาวเมืองทำตามจริยธรรมและสร้างกลุ่มสาวกของพีทาโกรัส จากนั้นพีทาโกรัสก็ได้เปิดสถานศึกษา โรงเรียนของพีทาโรกัสเปิดรับทั้งชายและหญิง แต่ผู้ที่จะเข้าร่วมจำเป็นต้องสละทรัพย์สิน กินอยู่แบบมังสวิรัตที่โรงเรียน และเรียกตัวเองว่ามาเทมาทิคอย (Mathematikoi) คนอื่นๆ ที่อยู่ในพื้นที่ใกล้เคียงก็สามารถเข้าเรียนได้ด้วย แต่จะไม่จำเป็นต้องสละทรัพย์สิน หรือใช้ชีวิตแบบมังสวิรัต
พวกพีทาโกเรียน
 สาวกของพีทาโกรัสได้ชื่อว่าพวก"พีทาโกเรียน" ผู้ที่เป็นนักคณิตศาสตร์และนักปราชญ์ที่บุกเบิกเรขาคณิต พวกพีทาโกเรียนยังมีความเชื่อเรื่องการกลับชาติมาเกิด และ ความเชื่อว่าตัวเลขเป็นธรรมชาติที่แท้จริงของทุกสิ่ง. พวกเขาปฏิบัติพิธีกรรมล้างมลทิน ปฏิบัติตามกฏการกินอาหาร และกฏอื่นๆ ซึ่งพวกเขาเชื่อว่าการปฏิบัติเช่นนี้จะทำให้พวกเขาเป็นอิสระจากวงจรการเกิดใหม่
สาวกของพีทาโกรัสได้ชื่อว่าพวก"พีทาโกเรียน" ผู้ที่เป็นนักคณิตศาสตร์และนักปราชญ์ที่บุกเบิกเรขาคณิต พวกพีทาโกเรียนยังมีความเชื่อเรื่องการกลับชาติมาเกิด และ ความเชื่อว่าตัวเลขเป็นธรรมชาติที่แท้จริงของทุกสิ่ง. พวกเขาปฏิบัติพิธีกรรมล้างมลทิน ปฏิบัติตามกฏการกินอาหาร และกฏอื่นๆ ซึ่งพวกเขาเชื่อว่าการปฏิบัติเช่นนี้จะทำให้พวกเขาเป็นอิสระจากวงจรการเกิดใหม่
พวกพีทาโกรัสยังเชื่ออีกเรื่องความเสมอภาคของชายและหญิง พีทาโกรัสเองริเริ่มโรงเรียนของเขาพร้อมด้วยภรรยาของเขา ทีอาโน (Theano) และหลังจากที่พีทาโกรัสได้ตายไปแล้ว ทีอาโนและลูกได้สอนต่อที่โรงเรียนของพีทาโกรัส
พวกพีทาโกเรียนปฏิบัติต่อทาสอย่างดี และสัตว์มีฐานะเป็นสิ่งมีชีวิตที่มีวิญญาณ พวกพีทาโกเรียนยังเชื่ออีกว่าการชำระล้างวิญญาณที่สูงที่สุดคือ"ปรัชญา" หลายสิ่งที่พวกพีทาโกเรียนปฏิบัตินั้นเหมือนกันกับสิ่งที่พวกเจนในอินเดียปฏิบัติ ทำให้ผู้เชี่ยวชาญหลายท่านสันนิษฐานว่าพีทาโกรัสเองเคยได้ศึกษาอยู่กับพวกเจนในอินเดีย
ทฤษฎีบทพีทาโกรัส
ในวิชาคณิตศาสตร์ ทฤษฎีบทพีทาโกรัส แสดงความสัมพันธ์ในเรขาคณิตแบบยุคลิด ระหว่างด้านทั้งสามของสามเหลี่ยมมุมฉาก กำลังสองของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของอีกสองด้านที่เหลือ ในแง่ของพื้นที่ กล่าวไว้ดังนี้
ในสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของสี่เหลี่ยมที่มีด้านเป็นด้านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมที่มีด้านเป็นด้านประชิดมุมฉากของสามเหลี่ยมมุมฉากนั้น |
ทฤษฎีบทดังกล่าวสามารถเขียนเป็นสมการสัมพันธ์กับความยาวของด้าน a, b และ c ได้ ซึ่งมักเรียกว่า สมการพีทาโกรัส ดังด้านล่าง[1]
 ทฤษฎีบทพีทาโกรัสตั้งตามชื่อนักคณิตศาสตร์ชาวกรีก พีทาโกรัส ซึ่งถือว่าเป็นผู้ค้นพบทฤษฎีบทและการพิสูจน์[2][3] แม้จะมีการแย้งบ่อยครั้งว่า ทฤษฎีบทดังกล่าวมีมาก่อนหน้าเขาแล้ว มีหลักฐานว่านักคณิตศาสตร์ชาวบาบิโลนเข้าใจสมการดังกล่าว แม้ว่าจะมีหลักฐานหลงเหลืออยู่น้อยมากว่าพวกเขาปรับให้มันพอดีกับกรอบคณิตศาสตร์[4][5]
ทฤษฎีบทพีทาโกรัสตั้งตามชื่อนักคณิตศาสตร์ชาวกรีก พีทาโกรัส ซึ่งถือว่าเป็นผู้ค้นพบทฤษฎีบทและการพิสูจน์[2][3] แม้จะมีการแย้งบ่อยครั้งว่า ทฤษฎีบทดังกล่าวมีมาก่อนหน้าเขาแล้ว มีหลักฐานว่านักคณิตศาสตร์ชาวบาบิโลนเข้าใจสมการดังกล่าว แม้ว่าจะมีหลักฐานหลงเหลืออยู่น้อยมากว่าพวกเขาปรับให้มันพอดีกับกรอบคณิตศาสตร์[4][5]
ทฤษฎีบทดังกล่าวเกี่ยวข้องกับทั้งพื้นที่และความยาว ทฤษฎีบทดังกล่าวสามารถสรุปได้หลายวิธี รวมทั้งปริภูมิมิติที่สูงขึ้น ไปจนถึงปริภูมิที่มิใช่แบบยูคลิด ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมมุมฉาก และอันที่จริงแล้ว ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมเลยก็มี แต่เป็นทรงตัน n มิติ ทฤษฎีบทพีทาโกรัสดึงดูดความสนใจจากนักคณิตศาสตร์เป็นสัญลักษณ์ของความยากจะเข้าใจในคณิตศาสตร์ ความขลังหรือพลังปัญญา มีการอ้างถึงในวัฒนธรรมสมัยนิยมมากมายทั้งในวรรณกรรม ละคร ละครเพลง เพลง สแตมป์และการ์ตูน
ตามที่ได้กล่าวไปแล้วข้างต้น หาก c แทนความยาวด้านตรงข้ามมุมฉาก และ a และ b แทนความยาวของอีกสองด้านที่เหลือแล้ว ทฤษฎีบทพีทาโกรัสจะสามารถเขียนในรูปสมการพีทาโกรัสได้ดังนี้
ทฤษฎีบทดังกล่าวสามารถกล่าวโดยสรุปได้เป็นกฎของโคซายน์ ซึ่งเมื่อให้ความยาวของด้านทั้งสองและขนาดของมุมระหว่างด้านนั้นมา จะสามารถคำนวณหาความยาวด้านที่สามของสามเหลี่ยมใด ๆ ได้ ถ้ามุมระหว่างด้านเป็นมุมฉาก กฎของโคซายน์จะย่อลงเหลือทฤษฎีบทพีทาโกรัส
การพิสูจน์
ทฤษฎีบทพีทาโกรัสอาจเป็นทฤษฎีบทที่รู้จักกันว่ามีการพิสูจน์มากกว่าทฤษฎีบทอื่น หนังสือ The Pythagorean Proposition มีการพิสูจน์มากถึง 370 แบบ[6]
บทกลับของทฤษฎีบทปีทาโกรัส
กำหนด a, b และ c เป็นจำนวนจริงบวกที่จะมีสามเหลื่ยมมุมฉากหนึ่งรูปที่มีความยาวด้านเท่ากับสามจำนวนนั้น และสามเหลี่ยมนั้นจะมีมุมฉากระหว่างด้าน a และ b
สำหรับสามเหลี่ยมใด ๆ ที่มีด้าน a, b และ c ถ้าแล้วมุมระหว่าง a กับ b จะวัดได้ 90°
ถ้าในสามเหลี่ยมรูปหนึ่ง สี่เหลี่ยมบนด้านหนึ่งเท่ากับผลรวมของสี่เหลี่ยมบนอีกสองด้านที่เหลือของสามเหลี่ยมแล้ว แล้วมุมที่รองรับด้านทั้งสองที่เหลือของสามเหลี่ยมนั้นจะเป็นมุมฉาก
กำหนดสามเหลี่ยม ABC มีด้านสามด้านที่มีความยาว a,b และ c และ
 เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย
เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วยจากบทพิสูจน์ของบทกลับของทฤษฎีบทปีทาโกรัส เราสามารถนำไปหาว่ารูปสามเหลี่ยมใด ๆ เป็นสามเหลี่ยมมุมแหลม, มุมฉาก หรือ มุมป้าน ได้ เมื่อกำหนดให้ c เป็นความยาวของด้านที่ยาวที่สุดในรูปสามเหลี่ยม
- ถ้า
 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก - ถ้า
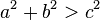 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม
ผลงาน
ขอขอบคุณแหล่งที่มาที่ใช้ในการศึกษา
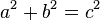



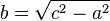



 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน 

ไม่มีความคิดเห็น:
แสดงความคิดเห็น